The topic to which I have been asked to address myself is a difficult one, if one is to avoid the trivial and the banal. And, moreover, my knowledge and my experience, such as they are, compel me to limit myself entirely to the theoretical aspects of the physical sciences - limitations, most serious. I must, therefore, begin by asking for your patience and your forbearance.
All of us are sensitive to Nature's beauty. It is not unreasonable that some aspects of this beauty are shared by the natural sciences. But one may ask the question as to the extent to which the quest for beauty is an aim in the pursuit of science. On this question, Poincaré is unequivocal. In one of his essays he has written:
“The Scientist does not study nature because it is useful to do so. He studies it because he takes pleasure in it; and he takes pleasure in it because it is beautiful. If nature were not beautiful, it would not be worth knowing and life would not be worth living. […] I mean the intimate beauty which comes from the harmonious order of its parts and which a pure intelligence can grasp.”
And Poincaré goes on to say, “It is because simplicity and vastness are both beautiful that we seek by preference simple facts and vast facts; that we take delight, now in following the giant courses of the stars, now, in scrutinizing with a microscope that prodigious smallness which is also a vastness, and, now, in seeking in geological ages the traces of the past that attracts us because of its remoteness.”
Commenting on these observations of Poincaré, J.W.N. Sullivan, the author of perceptive biographies of both Newton and Beethoven, wrote (in the Athenium for May 1919):
“Since the primary object of the scientific theory is to express the harmonies which are found to exist in nature, we see at once that these theories must have aesthetic value. The measure of the success of a scientific theory is, in fact, a measure of its aesthetic value, since it is a measure of the extent to which it has introduced harmony in what was before chaos.
It is in its aesthetic value that the justification of the scientific theory is to be found, and with it the justification of the scientific method. Since facts without laws would be of no interest, and laws without theories would have, at most, only a practical utility, we see that the motives which guided the scientific man are, from the beginning, manifestations of the aesthetic impulse. […] The measure in which science falls short of art is the measure in which it is incomplete as science.”

In a perceptive essay on Art and Science , the distinguished art critic, Roger Fry (who may be known to some of you through Virginia Woolf 's biography of him), begins by quoting Sullivan and continues:
Sullivan boldly says: "It is in its aesthetic value that the justification of the scientific theory is to be found and with it the justification of the scientific method." I should like to pose to S. [Sullivan] at this point the question whether a theory that disregarded facts would have equal value for science with one which agreed with facts. I suppose he would say No; and yet so far as I can see there would be no purely aesthetic reason why it should not.
I shall return to this question which Roger Fry raises and suggest an answer different from what Fry presumes that Sullivan would have given. But I shall pass on now to Fry's observations comparing the impulses of an artist and of a scientist.
“From the merest rudiments of pure sensation up to the highest efforts of design, each point in the process of art is inevitably accompanied by pleasure: it cannot proceed without it. […] It is also true that the recognition of inevitability in thought is normally accompanied by pleasurable emotion; and that the desire for this mental pleasure is the motive force which impels to the making of scientific theory. In science the inevitability of the relations remains equally definite and demonstrable, whether the emotion accompanies it or not, whereas, in art, an aesthetic harmony simply does not exist without the emotional state. The harmony in art is not true unless it is felt with emotion. In art the recognition of relations is immediate and sensational perhaps we ought to consider it as curiously akin to those cases of mathematical geniuses who have immediate intuition of mathematical relations which it is beyond their powers to prove.
Let me pass on from these generalities to particular examples of what scientists have responded to as beautiful.
My first example is related to Fry's observation with respect to what mathematical geniuses perceive as true with no apparent cause. The Indian mathematician, Srinivasa Ramanujan (whose dramatic emergence into mathematical fame in 1915 may be known to some of you) left a large number of notebooks (one of which was discovered only a few years ago). In these notebooks Ramanujan has recorded several hundred formulae and identities. Many of these have been proved only recently by methods which Ramanujan could not have known. G. N. Watson, who spent several years of his life proving many of Ramanujan's identities, has written :
“The study of Ramanujan' s work and the problem to which it gives rise, inevitably recalls to mind Lamé's remark that, when reading Hermite's papers on modular functions, "on a la chair de poule." I would express my own attitude with more prolixity by saying that such a formula as,
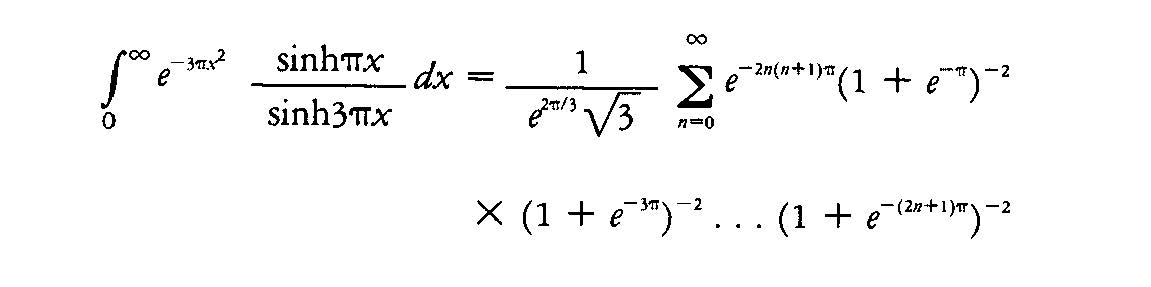 gives me a thrill which is indistinguishable from the thrill which I feel when I enter the Sagrestia Nuova of Capelle Medicee and see before me the austere beauty of "Day," "Night," "Evening," and "Dawn" which Michelangelo has set over the tombs of Giuliano de' Medici and Lorenzo de' Medici.
gives me a thrill which is indistinguishable from the thrill which I feel when I enter the Sagrestia Nuova of Capelle Medicee and see before me the austere beauty of "Day," "Night," "Evening," and "Dawn" which Michelangelo has set over the tombs of Giuliano de' Medici and Lorenzo de' Medici.
An example of a very different kind is provided by Boltzmann's reaction to one of Maxwell's papers on the dynamical theory of gases in which Maxwell shows how one can solve exactly for the transport coefficients in a gas in which the intermolecular force varies as the inverse fifth power of the intermolecular distance. Here is Boltzmann:
“Even as a musician can recognize his Mozart, Beethoven, or Schubert after hearing the first few bars, so can a mathematician recognize his Cauchy, Gauss, Jacobi, Helmholtz, or Kirchhoff after the first few pages. The French writers reveal themselves by their extreme formal elegance, while the English, especially Maxwell, by their dramatic sense. Who, for example, is not familiar with Maxwell's memoirs on his dynamic theory of gases? […] The variations of the velocities are, at first, developed majestically; then from one side enter the equations of state; and from the other side, the equations of motion in a central field. Ever higher soars the chaos of formulae. Suddenly, we hear, as from kettle drums, the four beats "put n = 5." The evil spirit V (the relative velocity of the two molecules) vanishes; and, even as in music, a hitherto dominating figure in the bass is suddenly silenced, that which had seemed insuperable has been overcome as if by a stroke of magic. […] This is not the time to ask why this or that substitution. If you are not swept along with the development, lay aside the paper. Maxwell does not write programme music with explanatory notes. […] One result after another follows in quick succession till at last, as the unexpected climax, we arrive at the conditions for thermal equilibrium together with the expressions for the transport coefficients. The curtain then falls!”
I have started with these two simple examples to emphasize that one does not have to go to the largest canvasses to find beauty in science. But the largest canvasses do provide the best examples. I shall consider two of them.
Einstein's discovery of the general theory of relativity has been described by Hermann Weyl as a supreme example of the power of speculative thought, while Landau and Lifshitz consider the theory as probably the most beautiful of all existing physical theories. And Einstein himself wrote at the end of his first paper announcing his field equations: “Scarcely anyone who fully understands this theory can escape from its magic.”
I shall return later to consider wherein the source of this magic lies. Meantime, I want to contrast, in parallel with Einstein's expressed reaction to his theory, the feelings of Heisenberg at the moment of his discovery of quantum mechanics. We are fortunate in having Heisenberg's own account. He writes:
“It had become clear to me what precisely had to take the place of the Böhr-Sommerfeld quantum conditions in an atomic physics working with none but observable magnitudes. It also became obvious that with this additional assumption, I had introduced a crucial restriction into the theory. Then I noticed that there was no guarantee that the principle of the conservation of energy would apply. […] Hence I concentrated on demonstrating that the conservation law held; and one evening I reached the point where I was ready to determine the individual terms in the energy table [Energy Matrix]. When the first terms seemed to accord with the energy principle, I became rather excited, and I began to make countless arithmetical errors. As a result, it was almost three o'clock in the morning before the final result of my computations lay before me. The energy principle had held for all the terms, and I could no longer doubt the mathematical consistency and coherence of the kind of quantum mechanics to which my calculations pointed. At first, I was deeply alarmed. I had the feeling that, through the surface of atomic phenomena, I was looking at a strangely beautiful interior, and felt almost giddy at the thought that I now had to probe this wealth of mathematical structure nature had so generously spread out before me.
In the context of these statements by Einstein and by Heisenberg on their discoveries, it is of interest to recall the following conversation between Heisenberg and Einstein which Heisenberg has recorded. Here is an extract:
“If nature leads us to mathematical forms of great simplicity and beauty – by forms, I am referring to coherent systems of hypotheses, axioms, etc. – to forms that no one has previously encountered, we cannot help thinking that they are "true," that they reveal a genuine feature of nature. You must have felt this too: the almost frightening simplicity and wholeness of the relationships which nature suddenly spreads out before us and for which none of us was in the least prepared.”
These remarks of Heisenberg find an echo in the following lines of Keats: “Beauty is truth, truth is beauty – that is all Ye know on earth, and all ye need to know.”
At this point, I should like to return to Hoger Fry's question, I quoted earlier, namely, what one should make of a theory which is aesthetically satisfying but which one believes is not true. Freeman Dyson has quoted Weyl as having told him: “In my work, I have always tried to unite the true with the beautiful; but when I had to choose one or the other, I usually chose the beautiful.”
I inquired of Dyson whether Weyl had given an example of his having sacrificed truth for beauty. I learned that the example which Weyl gave was his gauge theory of gravitation which he had worked out in his Raum-Zeit-Materoie. Apparently, Weyl became convinced that this theory was not true as a theory of gravitation; but still it was so beautiful that he did not wish to abandon it and so be kept it alive for the sake of beauty. But much later, it did turn out that Weyl's instinct was right after all, when the formalism of gauge invariance was incorporated into quantum electrodynamics.
Another example which Weyl did not mention, but to which Dyson drew attention is Weyl's two-component relativistic wave equation of the neutrino. Weyl discovered this equation and the physicists ignored it for some thirty years because it violated parity invariance. And again, it turned out that Weyl's instincts were right.
We have evidence, then, that a theory developed by a scientist, with an exceptionally well-developed aesthetic sensibility, can turn out to be true even if, at the time of its formulation, it appeared not to be so. As Keats wrote a long time ago, “What the imagination seizes as beauty must be truth - whether it existed before or not.” It is, indeed, an incredible fact that what the human mind, at its deepest and most profound, perceives as beautiful finds its realization in external nature. What is intelligible is also beautiful.
We may well ask; how does it happen that beauty in the exact sciences becomes recognizable even before it is understood in detail and before it can be rationally demonstrated? In what does this power of illumination consist?
These questions have puzzled many thinkers from the earliest times. Thus, Heisenberg has drawn attention, precisely in this connection, to the following thought expressed by Plato in the Phaedrus: “The soul is awestricken and shudders at the sight of the beautiful, for it feels that something is evoked in it that was not imparted to it from without by the senses, but has always been already laid down there in the deeply unconscious region.”
The same thought is expressed in the following aphorism of David Hume: “Beauty in things exists in the mind which contemplated them.”
Kepler was so struck by the harmony of nature as revealed to him by his discovery of the laws of planetary motion that in his Harmony of the World, he wrote:
“Now, it might be asked how this faculty of the soul, which does not engage in conceptual thinking and can therefore have no prior knowledge of harmonic relations, should be capable of recognizing what is given in the outward world. To this, I answer that all pure Ideas, or archetypal patterns of harmony, such as we are speaking of, are inherently present in those who are capable of apprehending them. But they are not first received into the mind by a conceptual process, being the product, rather, of a sort of instinctive intuition and innate in those individuals.”
More recently, Pauli, elaborating on these ideas of Kepler, has written: “The bridge, leading from the initially unordered data of experience to the Ideas, consists in certain primeval images pre-existing in the soul the archetypes of Kepler. These primeval images should not be located in consciousness or related to specific rationally formulizable ideas. It is a question, rather, of forms belonging to the unconscious region of the human soul, images of powerful emotional content, which are not thought, but beheld, as it were pictorially. The delight one feels, on becoming aware of a new piece of knowledge, arises from the way such pre-existing images fall into congruence with the behavior of the external objects […]” Pauli concludes with “One should never declare rational formulation are that theses laid down by rational formulation are the only possible presuppositions of human reason.”
This congruence between pre-existing images and external reality, to which Pauli refers, once intensely experienced appears to have the consequence that it develops over-confidence in judgment and values in the person who has had such an experience. For otherwise, how can one understand statements, such as these, made by some of the great scientists:
"It is thermodynamics gone mad," by Lord Kelvin, one of the founders of thermodynamics, commenting on Boltzmann's derivation of Stefan's law and Wien's derivation of his displacement law.
"You look at it from the point of view of the star; I look at it from the point of view of Nature," by Eddington in a controversial discussion with me.
"I disagree with most physicists at the present time just at this point," by Dirac in the context of his views on the extant methods of renormalization in quantum electrodynamics.
"It really looked as if, for the first time, we had a framework wide enough to include the entire spectrum of elementary particles and their interactions fulfilling my dream of 1933," by Heisenberg in 1957 in the context of his ill-fated collaboration with Pauli on a unified field theory.
"God does not throw dice," by Einstein; or, even more provokingly, "When judging a physical theory, I ask myself, whether I would have made the Universe in that way, had I been God," also by Einstein.
In the context of these last statements by Einstein, it may be well to remember Bohr's remonstrance that “Nor is it our business to prescribe to God how he should run the world!”
Perhaps it is in terms of this over-confidence that one must try to understand the comparative sterility of once great minds. For as Claude Bernard has said, “Those who have an excessive faith in their ideas are not fitted to make discoveries.”
I am clearly treading on dangerous ground. But it does provide me the opportunity to draw attention to a fact which has been a source of considerable puzzlement to me: it concerns the very different ways – at least, so they seem to me – in which great writers, poets, and musicians on the one hand and great scientists on the other, appear to grow and to mature.
It is not uncommon that in considering the works of a great writer or a great composer one distinguishes an early, a middle, and a late period. And it is almost always the case that the progression from the early, to the middle, and to the late periods is one of growing depth and excellence. In some cases, as in the cases of Shakespeare and Beethoven, the latest works are the greatest. This fact is forcibly described by J. Dover Wilson in his delineation of the growth of Shakespeare's art in his great tragedies.
From 1601 to 1608 he is absorbed in tragedy; and the path he treads during these eight years may be likened to a mountain track which, rising gently from the plain, grows ever narrower, until at the climax of the ascent, it dwindles to the thinnest razor-edge, a glacial arete, with the abyss on either band, and then once again grows secure for foothold as it broadens out and gradually descends into the valley beyond.
Eight plays compose this tragic course. The first, Julius Caesar, written a little before the tragic period proper, is a tragedy of weakness not of evil. In Hamlet the forces of evil are active and sinister, though still the prevailing note is weakness of character. Othello gives us Shakespeare's earliest creation of a character wholly evil, and at the same time Iago's victim is blameless – human weakness is no longer allowed to share the responsibility with heaven. King Lear carries us right to the edge of the abyss, for here horror is piled upon horror and pity on pity, to make the greatest monument of human misery and despair in the literature of the world. Shakespeare came very near to madness in Lear.
Yet he pushed forward: Macbeth, Antony and Cleopatra (one of the very greatest of Shakespeare's plays), and Coriolanus followed in succession. And Dover Wilson asks: “How did Shakespeare save his soul alive in this, one of the most perilous and arduous adventures ever undertaken by the spirit of man?” Shakespeare survived; and he survived only to follow his great tragedies by those wonderful plays, Winter's Tale and Tempest.
I am afraid that I have, perhaps, digressed a little too long in detailing to you the growth of Shakespeare's art. But I did want to emphasize to you the magnitude of that growth. And I am sure that one can say very similar things about Beethoven's late compositions which include the Hammerklavier Sonata, the Missa Solemnis, and above all, his last quartets.

While Shakespeare and Beethoven are probably unique in treading the razor-edge at the end of their lives and surviving, there are others who illustrate, at a somewhat more modest level, the same consistent ascent to higher peaks of accomplishment. But I am not aware of a single instance of a scientist of whom the same can be said. His early successes are often his last successes. (I am here excluding the cases of those who, like Coates, Galois, Abel, Ramanujan, and Majorana, died in their youth. In these cases, we do not know how they may have fared had they lived past their prime.) In any event, he seems unable to sustain a constant and a continuous ascent. Why is this the case? I shall not, however, attempt to answer this question but pass on to some more concrete considerations.
The question to which I now wish to address myself is how one may evaluate scientific theories as works of art in the manner of literary or art criticisms. The case of general relativity provides a good example, since almost everyone is agreed that it is a beautiful theory. I think it is useful to inquire wherein the source of this beauty lies. It will not do, I think, to dismiss such an inquiry with an assertion such as Dirac's (made in a different context): “[Mathematical beauty] cannot be defined any more than beauty in art can be defined, but which people who study mathematics usually have no difficulty in appreciating.”
Nor do I think that one should be satisfied with a remark such as Born's “It [the general theory of relativity] appeared to me like a great work of art, to be enjoyed and admired from a distance.” (Parenthetically, may I say, quite frankly, that I do not know what to make of Born 's remark. Has the general theory of relativity to be admired only from a distance? Does it not require study and development like any other branch of the physical sciences?) In spite of the inherent difficulties which beset such discussions, I shall attempt to clarify why the general theory of relativity appeals to our aesthetic sense and why we consider it as beautiful. For this purpose, it is necessary to adopt some criteria for beauty. I shall adopt two.
The first is the criterion of Francis Bacon: “There is no excellent beauty that hath not some strangeness in the proportion!” (Strangeness, in this context, has the meaning "exceptional to a degree that excites wonderment and surprise.") The second criterion, as formulated by Heisenberg, is complementary to Bacon's: “Beauty is the proper comformity of the parts to one another and to the whole.”
That the general theory of relativity has some strangeness in the proportion, in the Baconian sense, is manifest. It consists primarily in relating, in juxtaposition, two fundamental concepts which had, till then, been considered as entirely independent: the concepts of space and time, on the one hand, and the concepts of matter and motion on the other. Indeed, as Pauli wrote in 1919 “ The geometry of space-time is not given; it is determined by matter and its motion.”
In the fusion of gravity and metric that followed, Einstein accomplished in 1915 what Riemann had prophesied in 1854, namely, that the metric field must be causally connected with matter and its motion. Perhaps the greatest strangeness in the proportion consists in our altered view of spacetime. As Eddington wrote: “Space is not a lot of points close together; it is a lot of distances interlocked.”
There is another aspect of Einstein's founding of his general theory of relativity that continues to be a marvel. It is this. We can readily concede that Newton's laws of gravitation require to be modified to allow for the finiteness of the velocity of light and to disallow instantaneous action at a distance. With this concession, it follows that the deviation of the planetary orbits from the Newtonian predictions must be quadratic in v/c where v is a measure of the velocity of the planet in its orbit and c is the velocity of light. In planetary systems, these deviations, even in the most favorable cases, can amount to no more than a few parts in a million. Accordingly, it would have been entirely sufficient if Einstein had sought a theory that would allow for such small deviations from the predictions of the Newtonian theory by a perturbative treatment. That would have been the normal way. But that was not Einstein's way: he sought, instead, for an exact theory. And he arrived at his field equations by qualitative arguments of a physical nature combined with an unerring sense for mathematical elegance and simplicity. The fact that Einstein was able to arrive at a complete physical theory by such speculative thought is the reason why, when we follow his thoughts, we feel as "though a wall obscuring truth has collapsed" (Weyl).
The foregoing remarks apply only to the foundations of the theory leading to the field equations. We must now ask, whether on further examination, the theory satisfies the second criterion for beauty, namely, "the conformity of the parts to one another, and to the whole." The theory most abundantly satisfies this criterion while revealing at every stage a "strangeness in the proportion." Let me give a few illustrations.
Consider, first, the solutions which the general theory of relativity allow for black holes. As is known, black holes partition the three-dimensional space into two regions, an inner region, bounded by a smooth two-dimensional null-surface, which (the inner region) is incommunicable to the space outside which is asymptotically flat. It is a startling fact that with these very simple and necessary restrictions, the general theory allows for stationary black holes a single unique two-parameter family of solutions. This is the Kerr family in which the two parameters are the mass and the angular momentum of the black hole. What is even more remarkable, the metric for this family of solutions is explicitly known. The Kerr metric is axisymmetric and represents a black hole rotating about the axis of symmetry.
The axisymmetric character of the Kerr geometry clearly guarantees that the energy of a test particle describing a geodesic, as well as its component of the angular momentum about the axis of symmetry, will be conserved. In addition to these two conserved quantities, the Kerr geometry unexpectedly allows for the test particle a third conserved quantity (discovered by Brandon Carter). In consequence, the Hamilton-Jacobi equation, governing the motion of a test particle, is separable in its variables; and the solution of the geodesic equations can be reduced to quadratures. This was surprising enough. But what is even more surprising is that all the equations of mathematical physics –the scalar wave equation, Maxwell's equations, Dirac's equation, and the equations governing the propagation of gravitational waves– all, are separable in Kerr geometry (even as they are in Minkowskian geometry) and can, therefore, be solved explicitly.
One experiences similar astonishment when we realize that the singularity theorems of Penrose and Hawking require that our universe must necessarily have originated in a singularity and that, in consequence, we are compelled to contemplate the nature of the physical processes that will occur at densities of the order of 1093 gms/cm3, in volumes with linear dimensions of the order of 10-33 cm, and in time intervals of the order of 10-44 seconds – dimensions which must stagger even this audience. Or again, Hawking's theorem that the surface area of a black hole must always increase suggests the identification of the surface area with the thermodynamic entropy of the black hole; and this leads to an intimate connection between thermodynamics, geometry, and gravity. There is clearly no lack of strangeness in the proportion in all these!
Everything I have said so far is in conformity with the two criteria of beauty with which I started. But there is yet another aspect of the matter which remains to be considered.
When Henry Moore visited the University of Chicago some ten years ago, I had the occasion to ask him how one should view sculptures: from afar or from nearby. Moore's response was that the greatest sculptures can be viewed – indeed, should be viewed– from all distances since new aspects of beauty will be revealed in every scale. Moore cited the sculptures of Michelangelo as examples. In the same way, the general theory of relativity reveals strangeness in the proportion at any level in which one may explore its consequences. One illustration must suffice.
If one enlarges Einstein's equations to the Einstein-Maxwell equations, i.e., the field equations appropriate for space pervaded by an electromagnetic field, and seeks spherically symmetric solutions, one obtains a solution describing a black hole with a mass and an electric charge. This solution was discovered by Reissner and Nordström as a generalization of the well known one of Schwarzschild. Because of the charge of the black hole, it is clear that if an electromagnetic wave is incident on the black hole, a certain fraction of the incident electromagnetic energy will be reflected back in the form of gravitational waves. Conversely, if a gravitational wave is incident on the black hole, a certain fraction of the incident gravitational energy will be reflected back in the form of electromagnetic waves. The remarkable fact is that the two fractions are identically the same, i. e., for all frequencies. This result was not expected and the underlying cause for it is still not known. This example illustrates how strangeness in the proportion is revealed by the general theory of relativity at all levels of exploration. And it is this fact, more than any other, that contributes to the unparalleled beauty of the general theory of relativity.
So far, my remarks have been confined to what we may all concede as great ideas conceived by great minds. It does not, however, follow that beauty is experienced only in the context of great ideas and by great minds. This is no more true than that the joys of creativity are restricted to a fortunate few. They are, indeed, accessible to each one of us provided we are attuned to the perception of strangeness in the proportion and the conformity of the parts to one another and to the whole. And there is satisfaction also to be gained from harmoniously organizing a domain of science with order, pattern, and coherence. Examples of such organizations are Jacobi's Vorlesungen über Dynamik, Boltzmann's Vorlesungen über Gas Theorie, Sommerfeld's Atombau and Spektrallinen, Dirac's Principles of Quantum Mechanics, and the various gems of exposition which Schrodinger wrote in his later years. The translucence of the eternal splendor through material phenomena (of which Plotinus spoke) are made iridescent in these books.
May I conclude then by suggesting that each of us, in our own modest ways, can achieve satisfaction in our quest for beauty in science like the players in Virginia Woolf's The Waves: “There is a square; there is an oblong. The players take the square and place it upon the oblong. They place it very accurately; they make a perfect dwelling place. Very little is left outside. The structure is now visible; what was inchoate is here stated; we are not so various or so mean; we have made oblongs and stood them upon squares. This is our triumph; this is our consolation.”
S. Chandrasekhar, Truth and Beauty: Aesthetics and Motivations in Science (Chicago: University of Chicago Press, 1987), pp. 59-73.
