James Clerk Maxwell and the Equations of Light

Alongside Isaac Newton and Albert Einstein, James Clerk Maxwell (1831-1879) is considered one of the greatest scientists of our modern era. His work has transformed our understanding of the world, having a great impact on daily life. The following text by Thomas Forsyth Torrance was originally published in the volume Transformation and Convergence in the Frame of Knowledge (Belfast, 1984). A historian and philosopher of science, Torrance paints a quite authentic portrait of the Scottish physicist. Maxwell was the first to formulate, between 1860 and 1870, the four equations that describe the propagation of the electromagnetic field. Torrance’s text especially brings out the relationship between Maxwell’s personal life, his philosophical and religious convictions and his scientific work. These equations are elegant and symmetrical, for he believed they should mirror the beauty of nature. Building on Michael Faraday’s previous studies, Maxwell was the first to demonstrate that the electric and magnetic fields could be unified into one field and that the energy of the electromagnetic field propagated through empty space as waves. In doing so, he developed a complementary look at the theory of light, which up until then had been predominantly interpreted as if light were made by particles. In the 1980’s, Maxwell’s unification of the electromagnetic field would be followed by another important step of unification, confirmed on experimental bases, between the electro-magnetic interaction and the weak nuclear interaction. Today, a further unification which includes also the strong nuclear force is possible only on theoretical bases, leading to what we call Gran Unification theory (GUT).

James Clerk Maxwell was born in Edinburgh on June 13, 1831. He had begun his scientific education originally in the University of Edinburgh in 1847, and then in Cambridge in 1850. Four years later, he had finished his university studies and began his academic career, being named a fellow at Trinity College of Cambridge the following year. In 1856 he began teaching Natural Philosophy at King’s College in London. That position was followed by a long period of private life away from teaching, until in 1871 he accepted the chair of Experimental Physics at the University of Cambridge, where he directed the Cavendish Laboratory. He authored numerous publications, some scientific and others not, the first of which, On Faraday's lines of force, a treatise on electricity, he wrote at the age of 24. Although he initially dedicated his efforts to the theory of color and the problems of dynamics and thermodynamics, he is mainly known for his famous differential equations that describe the electromagnetic field. Maxwell was a man of broad philosophical interests and deep religious faith. He died in 1879 at Cambridge at just 48, after a serious illness.

Like Michael Faraday with whom he had such a deep affinity, clerk Maxwell was a very devout and humble Christian believer in the Reformed tradition. It is significant that in his article on Michael Faraday for the Encyclopaedia Britannica Clerk Maxwell made a point of referring to the other side of Faraday’s character which was «reserved for his friends, his family and his church», his public profession of faith and his opinion with respect to the relation between his science and his religion [The Scientific Papers of James Clerk Maxwell, edited by W. D. Niven, Cambridge, 1890, vol. 2, p. 792f]. What Clerk Maxwell recounted of Faraday there was very self-revealing. In a lecture before the Royal Institution in 1854 on the subject of mental education, Faraday felt constrained to conclude on a more personal note about his faith in God and the future life. After claiming «an absolute distinction between religious and ordinary belief he declared: “Yet even in heartly matters I believe that the invisible things of Him from the creation of the world are clearly seen, being understood by the things that are made, even His eternal power and Godhead”; and I have never seen anything incompatible between those things of man which can be known by the spirit of man which is within him, and those higher things concerning his future which he cannot know, by that spirit”. Then Faraday added a note to the effect that “These observations … are so immediately connected in their nature and origin with my own experimental life, considered either as cause or consequence, that I have thought the close of this volume may not be an unfit place for their reproduction» [The work to which Faraday referred was Experimental Research in Chemistry and Physics. London, 1859]

I. Maxwell: his philosophical approach to the scientific task

Clerk Maxwell considered that scientist engaged in this difficult but delicate task of combining the mathematical and the physical in his understanding of created nature was reproducing, as it were, the pattern of God's creative operation, or at least exhibiting «the essential constituents of the image of him who in the beginning created, not only the heaven and the earth, but the materials of which heaven and earth consist» [Scientific Papers, vol. 2, p. 377]. «Happy is the man», he wrote, «who can recognise in the work of to-day a connected portion of the work of life, and an embodiment of the work of Eternity. The foundations of his confidence are unchangeable, for he has been made a partaker of Infinity. He strenuously works out his daily enterprises, because the present is given him for a possession. Thus ought man to be an impersonation of the divine process of nature, and to show forth the union of the infinite with the finite, not slighting his temporal existence, remembering that in it only is individual action possible, nor yet shutting out from his view that which is eternal, knowing that time is a mystery which man cannot endure to contemplate until eternal Truth enlighten it» [Lewis Campbell and William Garnett, The Life of James Clerk Maxwell, with a selection from his correspondence and occasional writings and a sketch of his contributions to science. London, 1882. p. 200]. It was from deep within religious convictions of this kind that Clerk Maxwell found himself unceasingly compelled to be as faithful as possible to the inherent structure and dynamic configuration of the world as it came from the wisdom and power of the Creator, and was therefore determined to pursue a way of scientific thinking which would not allow the natural integration of things to break up in his handling of them. Along with his natural bent of mind that was the secret behind his insistent demand for embodied mathematics.

From his earliest days at Edinburgh Academy and Edinburgh University, as Richard Olson has rightly pointed out, Clerk Maxwell was deeply interested in the embodiment of geometrical patterns in the physical relations exhibited by nature in its static and dynamic forms. Thus in the essay on real analogies in nature he could instance the mathematical forms of crystals “bursting in upon us”, and add: «It is because we have blindly excluded the lessons of these singular bodies from the domain of human knowledge that we are still in doubt about the great doctrine that the only laws of matter are those which our minds fabricate, and the only laws of mind are fabricated for it by matter» [Campbell and Garnett, op. cit., p. 244]. Geometrical patterns are found, however, not only in rigid structures like crystals but in the dynamic relations and configurations found at all levels of being and motion in the universe which science must seek to bring to appropriate mathematical expression as far as that is possible. Thus in Clerk Maxwell's thought we have a clear rejection of the post-Kantian dualist and positivist outlook which he found firmly entrenched in the continental molecularist and determinist science as exhibited, for example, by Laplace. He severely questioned the analytical, atomistic and rather artificial interpretation of nature in terms of abstract mathematical symbols, necessary as they were in their proper place, for it had the effect not only of dissecting nature but of distorting the real dynamical relations that are all-important in nature’s actual behaviour and regular manifestations, and nowhere more than in the electromagnetic field.

It was typical of Clerk Maxwell, therefore, that he should determine to read no mathematics on the subject of electricity till he had first read through Faraday’s Experimental Researches in Electricity, especially when he became aware of the difference there was supposed to be between Faraday’s way of conceiving of phenomena and that of the mathematicians. That is to say, to use an expression of Clerk Maxwell’s friend, C. J. Monro, he refused to allow mathematical equations «to lead him by the nose», for, to say the least, that would tend to trap him in «the fallacy of insufficient interpretation» [Campbell and Garnett, op. cit., p. 378]. As Clerk Maxwell proceeded with the study of Faraday, however, he «perceived that his method of conceiving the phenomena was also a mathematical one, though not exhibited in the conventional form of mathematical symbols». Faraday conceived of all space as a field of force and with lines of force traversing space in his mind’s eye he saw a medium where the mathematicians saw only action at a distance, and so he sought the seat of electromagnetic phenomena in the real actions going on in the medium in which the lines of force belonging to bodies where in some sense part of them. Faraday concentrated on “physical relation” and “physical truth” and struggled through the constant interplay of experiment and theory to find a way of reasoning with “physical hypotheses” which would be true to the actual states of affairs disclosed in experimental research. Clerk Maxwell tells us that when he translated Faraday’s ideas into mathematical form, he found that «Faraday’s method resembled those in which we begin with the whole and arrive at the parts of the analysis, while the ordinary mathematical methods were founded on the principle of beginning with the parts and building up the whole by synthesis» [A Treatise on Electricity and Magnetism, vol. 1, p. ix; vol. 2 (529) p. 176f]. What was generally supposed to be “the natural method” was far from being that, whereas Faraday’s method was in fact more “primitive” and more “natural”. Convinced that there must be a mathematical method in which we proceed from the whole to the parts instead of from the parts to the whole, Clerk Maxwell produced his now famous “partial differential equations” which he claimed to belong essentially to the method which he called that of Faraday. This was a way of mathematical reasoning in unbroken correlation with the changing configuration in a field of force, that is “physical reasoning as distinguished from calculation”. «My aim», he explained in another context, «has been to present the mathematical ideas to the mind in an embodied form, as systems of lines or surfaces, and not as mere symbols, which can neither convey the same ideas nor readily adapt themselves to the phenomena to be explained» [Scientific Papers, vol. 1, p. 187].

Clerk Maxwell's scientific relationship with Michael Faraday thus proved to be immensely helpful. Faraday's physical and yet implicitly mathematical way of thinking in wholistic groups of continuous relations greatly reinforced Clerk Maxwell's own deep convictions about “embodied mathematics” and increased his dissatisfaction with merely analytical mathematics. Faraday also provided him with a significant foil for his own innovative work which combined a heuristic leap forward of the mind with a basic change in the nature of scientific knowledge. For Clerk Maxwell this meant that the truth of mathematical propositions, that is their integration with the intrinsic properties of matter and motion, or their “physical truth”, had to take primacy over their certainty, that is their formal validity in tautological symbolic systems which have no inherent bearing on the real world. Mathematical truths of this kind fully shared with the truths of nature a basically contingent character which can never be grasped in any final or necessary way. This imported a radical change in the axiomatic and epistemological substructure of physical science which was not really appreciated in the nineteenth century. It was, however, a signal illustration of Clerk Maxwell's own notion of a new mathesis, to which we have already alluded, namely, a quite fresh way of deriving knowledge in which new ideas are gained and developed under the power of nature's own self-revelation and in harmony with its dynamic process, one in which the scientific mind operates at all levels with the mutual involution of empirical and theoretical elements.

II. Realism and fields theory

We must now take up Clerk Maxwell's concept of the field for, together with his partial differential equations and integrations which apply throughout all space, it represents the most significant breakthrough in the advance of physical science between Newton and Einstein. Here once again we must trace his thought back to his early studies in Edinburgh, and to the root theological and philosophical ideas with which his mind became imbued, and not least the concept of relational thinking which he found, for example, in the teaching of Sir William Hamilton. Evidence for this is apparent in Clerk Maxwell's 1856 essay on analogy where he showed that analogical resemblances and differences are embedded in the structural patterns of nature throughout the universe. Analogies are sets of relations which bear upon each other and point beyond themselves and thus supply us with fundamental clues for heuristic inquiry beyond the limits of empirical and observational knowledge. Hence, he claimed, «in a scientific point of view the relation is the most important thing to know» [Campbell and Garnett, op. cit., p. 243]. Clerk Maxwell insisted, however, that the relations he referred to were not just imaginary or putative but real relations, relations that belong to reality as much as things do, for the inter-relations of things are, in part at least, constitutive of what they are. Being-constituting relations of this kind we may well speak of as “onto-relations”.

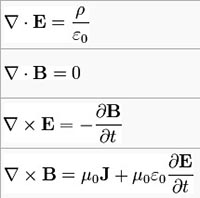Here we have a distinctive element in Scottish and Reformed theology which dates back to Duns Scotus' development of the concept of the person as it emerged from the Trinitarian teaching of Richard of St Victor, and was passed on through Duns Scotus' Commentaries on the Sentences of Peter Lombard to John Major in Paris and then to John Calvin and back, not least through the Syntagma Theologiae Christianae of Amandus Polanus, to Scotland. This was a theological mode of thinking which rejected the analytical, individualist notion of the person that was put forward by Boethius and Thomas Aquinas and was later reinforced and built into western social philosophy through the positivist individualism of John Locke and Auguste Comte who thought of persons as separated individuals connected through their external relations, rather like Newtonian particles. In the Reformed theological tradition the notion of the person is held to be controlled by the person­constituting and person-intensifying activity of God in the Incarnation, such that union with Christ becomes the ground for inter­ personal relations in the Church Relations between persons have ontological force and are part of what persons are as persons- they are real, person-constituting relations. That was the theology underlying Clerk Maxwell's concept of union with Christ and of inter-personal relations in Christ, which it was not his nature to isolate in some compartmentalised way from his understanding of real, ontological relations in the physical universe.

Clerk Maxwell also held, as we have already seen, that relations of this constitutive kind obtain as parts within a complex whole. They are not to be known through merely analytical operations but only through contemplation of the unifying whole and its interior relations. Even the fact that we number things in a series implies a previous act of intelligence in which we pick things out of the universe – «nature seems to have a certain horror of partition», he added. In other words, even the use of mathematical units in analysing a set of events implies a pre-analytical intuition of the whole. It is under the guidance and control of such an intuition that we may grasp something of the internal relations of a dynamic coherence inherent in nature without distorting dismemberment of it.

It was with these fundamental convictions and constitutive beliefs that Clerk Maxwell studied Faraday's researches which had resulted in the discovery of electromagnetic induction and the magnetic rotation of light rays, and had led him to put forward the idea of “moving lines of force” as a field of force having independent existence, in rather sharp contrast to the severely analytical approach of Newtonian science and its artificial notion of bodies acting instantaneously on each other at a distance and within empty uniform space and time. It is not surprising that Clerk Maxwell should have a deep affinity with this non-analytical wholistic approach and with the modes of thought which Faraday brought to it. Owing to the creative power of his own ideas, however, Clerk Maxwell was able to offer a quite distinctive mathematical interpretation of Faraday's physical hypotheses which went well beyond what contemporary science or mathematics had conceived, even beyond William Thomson's (Lord Kelvin's) appreciative development of Faraday's ideas, and rather startled Faraday himself. Writing rather later in life of Faraday’s scientific conceptions in relation to his own, Clerk Maxwell put his finger on the essence of the matter rather well. «He never considers bodies as existing with nothing between them but their distance, acting on one another according to some function of that distance. He conceives of all space as a field of force, the lines of force being in general curved, and those due to any body extending from it on all sides. He even speaks of lines of force belonging to a body as in some sense part of itself, so that in its action on distant bodies it cannot be said to act where it is not. This, however, is not a dominant idea with Faraday. I think he would rather have said that the field of space is full of lines of force, whose arrangement depends on that of bodies in the field, and that the mechanical and electrical action on each body is determined by the lines which abut on it» [A Treatise on Electricity and Magnetism, vol. 2, (529), p.177].

In these views Clerk Maxwell was presented with a rather fresh outlook upon the constitution of the universe as a vast field of matter and space governed by a basic unity of different forces, gravitational, electric, magnetic, chemical, etc., which were probably convertible into one another. This was a way of understanding nature which came rather close to the way in which Clerk Maxwell had himself come to appreciate dynamic and subtle connections manifested in created reality as it is continuously sustained by God.

Of particular significance for Clerk Maxwell was the way in which Faraday conceived of material bodies or particles, moving lines of force, and fields as merging into one another, which pointed to the idea that in the last resort bodies are so interconnected in fields of force that they must be regarded as the converging points of force rather than as discrete bodies in motion in empty space and time. Moreover since forces of this kind with real or physical existence do not interact in neighbourly relations, changes in the configuration of fields need time to take place through the interaction of forces, which points to the idea that time as well as space must belong to the vast field of force which is the underlying reality of all phenomena in the universe.

Faraday's interpretation of the dynamic behaviour of nature in terms of moving lines of force, as forces act upon contiguous forces progressively through the field, did not square with Newtoman laws but he on his part failed to determine the laws governing field of force. As Clerk Maxwell understood it, this notion of physical force interacting with force in a contiguous field, implying “the maxim that might is right”, demanded a mechanical explanation even if it was not a causalist or determinist explanation in the Newtonian sense. He tackled the problem in two distinct stages.

The first stage was marked by his paper On Physical Lines of Force which he wrote in 1856 although it was not published until five years later. His problem was to account for the way in which electric and magnetic forces or particles act on one another through external but contiguous relations, and to find a mathematical for its description. He saw that while integral equations are the appropriate mathematical expression for a theory of action between particles at a distance, differential equations must be used for a theory of action between contiguous parts of a medium. But in order to develop these equations he made use of a highly artificial and intricate mechanical model of magnetic vortices and electric currents, with “idle wheels” interposed between contiguous vortices, with a view to giving his physico-mathematical vision something distinct to work with in struggling to grasp the mechanics of the interaction of forces rather than causes in the electromagnetic field. This strange mechanical model was merely an ad hoc heuristic device but unsatisfactory as it was it enabled him to work out in the form of embodied mathematics a rigorous formalisation of the laws of the electromagnetic field, in the course of which he both derived the all-important partial differential equations and came up with his electromagnetic theory of light. In the very event of these brilliant achievements, however, Clerk Maxwell insisted that he did not put forward his imaginary mechanical model as «a mode of connexion existing in nature», but only as a provisional model to show that «such a mode of connexion ... is mechanically conceivable» [Scientific Papers, vol. 1, pp. 451-513]. That is to say, his paper On Physical Lines of Force was meant to provide a mechanical interpretation of electromagnetic phenomena in a form that would still harmonise with Newtonian mechanics. Nevertheless he was far from being happy with this approach, which perhaps explains why he held it back for several years. William Berkson has put the matter well. «Maxwell invented and worked with a theory he thought to be basically untenable, but he produced results amongst the most fruitful in the history of science». The effect of Clerk Maxwell's equations was to establish in an indubitable way the independent reality of the field but it also had the effect of altering his concept of the field as a medium of contiguous forces and demanding its reconsideration.

III. Dynamics and relational interpretation of Nature

This was the task he undertook in a second stage, with the publication of another work A Dynamical Theory of the Electromagnetic Field in 1865, which he had read before the Royal Society of London in December of the previous year. In this paper he embodied his partial differential equations in a thoroughly relational interpretation of the electromagnetic field without recourse to Newtonian mechanics. The way for that had been opened by his realisation that electromotive force is quite different from mechanical force, for it acts on electricity and not like mechanical force on the discrete bodies in which electricity resides, but now that realisation was much reinforced by the discovery of the identity in nature and speed between electromagnetic and light waves. This pointed to the fact that nature is ultimately governed by continuous fields of energy, even though the energy is manifest in two forms with respect to position and motion, in the dynamics of fields and in the mechanics of bodies in interaction. Clerk Maxwell's aim was not only to free his partial differential equations from the mechanical model but to derive them without recourse to mechanism. This is precisely what he managed to do, in showing that these equations enabled him to derive the structural laws of electromagnetic radiation and electromagnetic fields at any point in space and for any instant of time. As Einstein has expressed it: «The formulation of these equations is the most important event in physics since Newton's time, not only because of their wealth of content, but also because they form a pattern for a new type of law … Maxwell’s equations are laws representing the structure of the field … All space is the scene of these laws and not, as for mechanical laws, only points in which matter or charges are present» [Albert Einstein and Leopold Infeld, The evolution of Physics from Early Concepts to Relativity and Quanta, Clarion edit., New York, 1938, pp. 143, 146]. Thus in contrast to classical Newtonian science, the reconstruction of physical science brought about by Clerk Maxwell makes us conceive physical reality in terms of continuous, not just contiguous, fields of force throughout space and time.

Several comments about Clerk Maxwell's physical science may be worth making at this point.

(a) While Clerk Maxwell worked out a thoroughly relational account of the field in A Dynamical Theory of the Electromagnetic Field, he did not entirely discard his earlier mechanical account, but in accord with his view that there may be two ways of looking at things, brought both together in his major work A Treatise on Electricity and Magnetism (1873), constantly adjusting the focus of theory to the different levels of mechanical and dynamical interpretation, yet in such a way that it became clear that a mechanical interpretation represents a rather artificial approach which does not get at the real connections in nature, and can only be regarded, therefore, as a limiting case of a relational and dynamical account, and thus as having the status of a working model which must not be taken for more than it really is. The final effect of Clerk Maxwell's work, however, was that the continuous field appeared side by side with the material point as the representative of physical reality. This dualism, Einstein remarked, remained until his own day, disturbing as he found it for the orderly mind.

(b) Clerk Maxwell’s dynamical and relational theory of the field went beyond established observations and known experimental evidence, but the fact that the constant radiation of electromagnetic waves from a centre predicted by his equations was experimentally verified by Hertz showed that Clerk Maxwell's concept of the continuous field was consistent with reality. This was a significant event, for Clerk Maxwell's dynamical approach was so foreign to the atomistic and molecularist determinism of continental physics particularly that it was not taken seriously. Even Lord Kelvin on reading Clerk Maxwell's A Dynamical Theory f the Electromagnetic Field charged him with falling away into mysticism when he departed from the mechanical model. Through Hertz's discovery, however, as Max Planck pointed out, the greatest sensation was produced in the scientific world, for «the speculations of Maxwell were translated into fact and a new epoch of experimental and theoretical physics was begun».

(c) Doubtless from a strictly scientific point of view, the decisive factor in Clerk Maxwell's switch from a mechanical to a relational interpretation of the electromagnetic field was his derivation of partial differential equations as the natural expression of continuous fields, but behind that lay the masterful conviction which would not let him go, that nature as the God and Father of Jesus Christ had created it, does not behave in a mechanical way. That is to say, in the ultimate analysis it was Clerk Maxwell's Christian faith which exercised a regulative role in his scientific judgment and choice of concept and theory at this supreme juncture in the advance of physical science. The question had to be raised, if the electromagnetic field is not susceptible of mechanical explanation, how about the biological field? We do not know very much about Clerk Maxwell's reaction to evolution, but what we do have shows that he was uneasy about the mechanistic features of Darwinian theory. Of course in Clerk Maxwell's view all scientific theories no matter how rigorous fail to match the subtle and flexible modes of connection in created reality itself, but abstractive and mechanistic theories.

IV. New ideas of Space and Time

The last matter we must discuss is the implication of Clerk Maxwell's theories, and especially of his electromagnetic theory of light in a continuous field, for concepts of space and time. It is significant that there seems to be no evidence in Clerk Maxwell's papers and books for Newtonian container notions of space and time, while Kantian notions are resolutely brought into line with realist relations in the created universe. Questions of time and space were raised in his Cambridge essay on real analogies in nature when he discussed the close relations between the laws of nature and the constitution of the human intellect, but he concluded, as we have seen, that we have to operate with objectively controlled concepts, even though they are formulated in accordance with the laws of the human mind. That is to say, Clerk Maxwell did not work with absolute notions of time and space, either in the Newtonian or Kantian sense of “absolute” as unaffected by on-going empirical reality.

This concept of “objective truth” in scientific notions of time and space was deepened and reinforced in Clerk Maxwell’s rejection of action at a distance notions and his commitment to the independent reality of the continuous field in which we have to reckon with the fact that light waves travel trough space and take time to do so. This implies that spatial and temporal relations are inherent features in the dynamic structure of the field that underlines all the phenomena of physical reality. That is an implication that was mathematically established by Clerk Maxwell’s equations which describe the structure of the field at any point in space and for any instant of time. If these equations show us that rates of change in the configuration of fields involve time and space, they also show conversely that time and space are empirical features in the vast field of the universe. Moreover, in so far as Clerk Maxwell’s partial differential equations establish the independent reality and intelligibility of the continuous field, they show that the temporal and spatial structures of the field do not depend on the activity of the human observer in conceiving or measuring changes in the field. This has the conjunct effect of liberating notions of time and space from the dominance of the massive subjectivity in the Kantian metaphysical idea that they are a priori forms of man's sensory perception unaffected by empirical objectivity, and therefore of opening up the notions of time and space for radical reconsideration.

As we have already noted, Clerk Maxwell was impressed with the physical relevance of W. R. Hamilton's equations of motion and used them to help him derive an embodied-mathematical account of moving lines of force, but while he was aware of Riemannian four-dimensional geometry he does not seem to have discerned its implication for realist notions of space and time, let alone space-time, though he did apparently realise that a newer and deeper kind of continuity was being suggested. Evidently Maxwell's thought was on the brink of the next revolution that was to be brought about by Einstein in 1905 with his essay on special relativity, but perhaps Clerk Maxwell's hesitation to reject the notion of ether, even though it did not seem to have much importance for him, prevented him from seriously entertaining the idea that light waves might not need a medium through which to propagate themselves. However, enough has been said to show that Clerk Maxwell's dynamical theory of the electromagnetic field in which magnetism, electricity and light were unified in a single comprehensive theory, together with his partial differential equations, provided the basic material out of which, and in the light of the Lorentz transformations, Einstein claimed to have crystallised his theory of relativity which has transformed our notions of space and time.

There is no evidence to show that Clerk Maxwell directly allowed his Christian beliefs in the creation and the incarnation to influence his understanding of space and time, in the way that those cardinal doctrines affected the mind of the early Greek fathers who first put forward the relational notions of space and time, with which we work in science as in theology today. We know from his biographer that Clerk Maxwell loved to study the fathers and older divines, whom he preferred to modern theologians, which may indicate that he found their understanding of the created universe rather congenial. But it is certainly clear that the kind of physical science which he advocated is much more congenial to Christian theology than that which developed when absolute notions of space and time were arbitrarily clamped down upon the empirical world and had the effect of reducing understanding of it to a hard and closed mechanistic system. For Clerk Maxwell himself rigorous scientific inquiry and simple devout Christian faith were life-long partners, each in its own way contributing to the strength of the other. Hence it would not be unfitting to end this discussion of the bearing of Christian faith upon physical science with a prayer which Clerk Maxwell left among his papers.

«Almighty God, who hast created man in Thine own image, and made him a living soul that he might seek after Thee and have dominion over Thy creatures, teach us to study the works of Thy hands that we may subdue the earth to our use, and strengthen our reason for Thy service; and so to receive Thy blessed Word, that we may believe on Him whom Thou hast sent to give us knowledge of salvation and the remission of our sins. All which we ask in the name of the same Jesus Christ our Lord».

Bibliography

James Clerk Maxwell’s works: A Treatise on Electricity and Magnetism (1873), Dover, New York 1954; The Scientific Papers of James Clerk Maxwell, a cura di W.D. Niven, Cambridge 1890 (rist. Dover, New York 1965).

Studies about James Clerk Maxwell’s works: L. Campbell, W. Garnett, The Life of J.C. Maxwell and a selection from his correspondence and occasional writing and a sketch of his contributions to science, Macmillan and Co., London 1882; H. Poincaré, Électricité et optique,vol. I: Les théories de Maxwell et la théorie électromagnetique de la lumière, Georges Carré et C. Naud, Paris 1890-91; P. Duhem, Les theories electriques de J.Clerk Maxwell, etude historique et critique, Paris 1902; H. Lorentz, C. Maxwell’s electromagnetical theory, Cambridge University Press, Cambridge 1923; W. Berkson, Fields of Force. The development of a World View from Faraday to Einstein, Routledge, London 1974; C.W. Everitt, James Clerk Maxwell, Physicist and natural Philosopher, Charles Scribner’s, New York 1975; I. Tolstoy, James Clerk Maxwell, a Biography, University of Chicago Press, Chicago 1983; M. Goldman, The Demon in the Aether. The Story of James Clerk Maxwell, Paul Harris Publishing, Edinburgh 1983; P. Theerman, James Clerk Maxwell and Religion, “American Journal of Physics” 54 (1986), pp. 312-317; T.K. Simpson, Maxwell on the Electromagnetic Field, Rutgers University Press, New Brunswick 1997.